Los datos que nos proporciona un sistema de posicionamiento global como el norteamericano GPS acerca de una posición son tres: latitud, longitud y altura. En la presente entrada se van a mostrar diferentes maneras de medir la distancia entre dos posiciones tomando como referencia los datos de las coordenadas geográficas (latitud y longitud) de cada una, obviando la altura.

¿Por qué no se usa la altura?
Básicamente por dos razones:
- No tiene sentido intentar precisar el cálculo de la distancia incluyendo la altura porque la que proporciona un GPS no es fiable. Por otro lado, es posible obtener el dato de elevación para un punto en la superficie terrestre dadas las coordenadas de longitud y latitud, pero es una operación añadida que requiere la consulta a una base de datos.
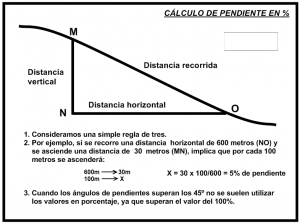
- Aunque se tuviera un dato preciso, la diferencia de altitud entre dos puntos apenas afecta a la distancia entre ellos: para una pendiente del 20% (que es bastante), la diferencia entre ladistancia horizontal (tramo ON) y la distancia recorrida (tramo OM) es menor del 2% (0,5% para una pendiente del 10%, cálculos hechos según el teorema de Pitágoras), que no justifica la complejidad que se introduciría de tener en cuenta las alturas de los puntos.
Modelos matemáticos
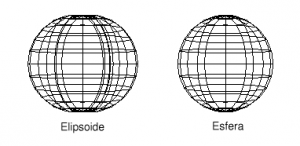
Para poder calcular la distancia entre dos puntos es necesario plantearse cómo están relacionados o más bien, cómo se pueden relacionar: ¿forman parte de una esfera?, ¿de un elipsoide (esfera achatada)?, ¿de un geoide?. La discusión acerca de la forma de la tierra es interesante, si bien no está claro quién fue el primero que descartó que fuera plana.
En el caso de utilizar fórmulas matemáticas para el cálculo de la distancia es necesario plantear un modelo que emule lo mejor posible la situación real ajustándose a criterios de limitaciones de potencia y tiempo de cálculo, quedando descartado el geoide.
Esfera
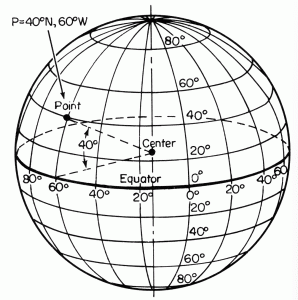
Es la aproximación más sencilla y también la que menos precisión obtiene, pero sin duda buena dada la simplicidad de la trigonometría esférica. Para el cálculo de la distancia entre dos puntos situados en la superficie de una esfera se utiliza la fórmula de Haversine, que es la más precisa frente a otras alternativas como la ley de los cosenos o el teorema de Pitágoras.
Elipsoide
Para un elipsoide existe un algoritmo iterativo conocido como fórmulas de Vincenty que proporciona una precisión extremadamente buena. El problema de este método es que al ser iterativo, puede provocar un bucle infinito en el cálculo para puntos casi antipodales.
Ejemplos
| Cálculo de distancias | Haversine | Vincenty |
|---|---|---|
| Puntos cercanos (consecutivos en actividad con Garmin Forerunner 210): (43.5291675º, -5.6391020º) y (43.5292752º, -5.6390161º) |
13,83 m | 13,835 m |
| Puntos relativamente alejados (lat, lon): (43.5372001º, -5.6370439º) y (43.5402668º, -5.6475824º) |
915,4 m | 917,392 m |
| Puntos alejados (lat, lon): Santiago Bernabéu (40.452961°, -3.688333°) y Camp Nou (41.380833°, 2.122778°) |
499,0 km | 500,15 km |
Hola, buenos dias
Alguien puede esclarecer una duda que tengo hace tiempo.
El calculo de las distancias recorridas la encuentro relativamente facil cuando los trayectos son en linea recta .
Ahora bien si yo subo una montaña i el sendero es accidentado i en el itinerario no hay mas alla de 2 0 3 metros en tinea recta, es decir tengo que hacer unsa multitud de curvas.
Si los puntos que emite el GPS son cada 8 a 20 metros i el trayecto es de 5 km, la distancia que me dira el receptor no sera OK.
Es así no ?
Pueden indicarme por email si estoy en lo cierto
Muchas gracias
Joan Blanch
Efectivamente la distancia que medirá el receptor GPS será inferior a la recorrida por usted en el caso de caminos sinuosos. Puede intentar minimizar el error aumentando la frecuencia con la que su dispositivo GPS registra los puntos, si bien a mayor frecuencia, mayor gasto de batería y mayor necesidad de espacio de almacenamiento de datos.
(imagen procedente de http://www.runtheline.com)
Buenos dias .
Estoy desarrollando una app Android en a cual se toma el punto gps y se almacena en la base de datos interna de la aplicación , de esta forma se llevan a cabo los registros, la siguiente vez que se use la app debe permitir a partir de la toma del punto extraer de la base de datos los punto mas cercanos a unos 10 metros , como creen que sea posible esta operación , en cuanto a calculos 🙂 de antemano Gracias
Restringiría la consulta en la base de datos para únicamente recuperar los puntos que se encuentren a la distancia solicitada, que sería la intersección de dos bandas (un cuadrado):
SELECT points FROM positions WHERE (latitude BETWEEN Lat-X AND Lat+X) AND (longitude BETWEEN Lon-X AND Lon+X) ;Siendo Lat, Lon las coordenadas del punto de referencia y X la diferencia de un punto situado a la distancia seleccionada a igualdad de la otra coordenada.
Y luego en código verificar que la distancia de esos puntos respecto al de referencia sea menor que los 10 metros seleccionados.
buenos dias, necesito hallar el área de un sitio determinado usando coordenadas de gps latitud y longitud pero necesito hallar la formula general o la matemática que hay implícita en cada calculo numérico si alguien me puede ayudar gracias
Lo más sencillo puede ser aproximar la superficie real con alguna figura geométrica conocida (una circunferencia, un cuadrado, un trapecio, etc.)
Si aun te interesa escribeme y te mando la hoja de excel
A mi me interesa, la hoja Excel para calcular las súpercies, conociendo las coordenadas. He visto el ofreciendo que le hiciste a Alejandro Zapata y es el que estaba buscando.
Saludos
Juan Llàcer
A cuantos km por hora te lo calcula ? Eje: si yo pongo el gps de mi casa hasta algun otro lugar me va a tirar la hora q tardo en llegar ahi.. Pero si yo voy mas rapido deberia ser menos el tiempo de llegada.. La pregunta seria a cuanto te calcula el gps 100km po hora o 130km por hora? La cuestion q me tengo q ir a un lado y juego con el tiempo y tengo 4 horas para llegar y el gps me dice q voy a tardar 4:31 min quiero saber a cuento lo calcula a esos 4:31
Una cosa es la distancia y otra el tiempo que se emplea en recorrerla.
La distancia entre dos puntos sobre la superficie de la Tierra no varía, pero el tiempo empleado depende del medio y el camino.
En el caso de la carretera, la duración teórica depende de la velocidad, que a su vez depende de la limitación legal y de la fluidez del tráfico del momento.
Buen día! Como estás? En principio muchas gracias por el aporte, fue de gran utilidad dado que no hay demasiada información sobre este tema.
La consulta que quisiera hacer , para ver si alguien puede abrirme un poco la cabeza al respecto es como podría medir la distancia de un punto geográfico a una recta. Explico para que, necesito mapear el recorrido de una máquina con un gps, y una vez que se realizo la primer pasada, trazo las rectas paralelas, luego necesito medir la distancia de un punto por donde va pasando la maquina a su recta para ver si esta volviendo a pisar el lugar por donde ya paso o si se está abriendo, me explico??
Espero la respuesta de alguien por favor auxilioo!!! Graciasss
La distancia entre un punto y una recta es la distancia más corta entre ese punto y un punto de la recta (en perpendicular).
Normalmente el sistema GPS no tiene la precisión de metros necesaria para calcular distancias con exactitud, pero algo que puede hacer es ver si la sucesión de puntos obtenidos sucesivamente son paralelos a la referencia.
Por ejemplo, en un sistema cartesiano (típicos ejes X e Y) puede darse una recta resultante de una serie de puntos: (1,0), (1,1), (1,2), etc. Si la siguiente serie de puntos es del estilo (3,0), (3,1), (4,2) no hace falta calcular distancias para saber que en la segunda serie ha habido un desvío.
Buenos Dias,
hay alguna forma sencilla de calcular el porcentaje de inclinacion o la pendiente entre dos puntos cercanos, conociendo las coordendas GPS de estos? Es para una App de MTB en la que sería interesante conocer la inclinación de la cuesta que esta subiendo en el instante mismo…
mil gracias saludos
quiero saber como se hace la operación para hallar la distancia entre dos coordenadas planas en metros